VELOCITY AND ACCELERATION OF CENTRE OF MASS OF A SYSTEM OF PARTICLES
If are the position vectors of masses , respectively, thle position vector of the centre of mass of the system of particles is given by
The velocity of the centre of mass is given by
The acceleration of the centre of mass is given by
If , then , i.e constant. Hence if no net external force acts on a system, its centre of mass will remain at rest or will move with a constant velocity.
The velocity of the centre of mass is given by
The acceleration of the centre of mass is given by
If , then , i.e constant. Hence if no net external force acts on a system, its centre of mass will remain at rest or will move with a constant velocity.
Head on elastic collision
(i) Linear momentum is conserved
$$ m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 $$
(ii) $K E$ is not conserved but initial $\mathrm{KE}$ is equal to final $\mathrm{KE}$
$$ \frac{1}{2} \mathrm{~m}_1 \mathrm{u}_1^2+\frac{1}{2} \mathrm{~m}_2 \mathrm{u}_2^2=\frac{1}{2} \mathrm{~m}_1 \mathrm{v}_1^2+\frac{1}{2} \mathrm{~m}_2 \mathrm{v}_2^2 $$
(iii) Rate of separation = Rate of approach i.e. $e=1$
$$ \Rightarrow \mathrm{u}_1-\mathrm{u}_2=\mathrm{v}_2-\mathrm{v}_1 $$
$$ m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 $$
(ii) $K E$ is not conserved but initial $\mathrm{KE}$ is equal to final $\mathrm{KE}$
$$ \frac{1}{2} \mathrm{~m}_1 \mathrm{u}_1^2+\frac{1}{2} \mathrm{~m}_2 \mathrm{u}_2^2=\frac{1}{2} \mathrm{~m}_1 \mathrm{v}_1^2+\frac{1}{2} \mathrm{~m}_2 \mathrm{v}_2^2 $$
(iii) Rate of separation = Rate of approach i.e. $e=1$
$$ \Rightarrow \mathrm{u}_1-\mathrm{u}_2=\mathrm{v}_2-\mathrm{v}_1 $$
Coefficient of restitution (Newton's law)
$$
e=-\frac{\text { velocity of separation along line of impact }}{\text { velocity of approach along line of impact }}=\frac{v_2-v_1}{u_1-u_2}
$$
Value of $e$ is 1 for elastic collision, 0 for perfectly inelastic collision and $0
Value of $e$ is 1 for elastic collision, 0 for perfectly inelastic collision and $0
LINEAR MOMENTUM
The linear momentum $\overrightarrow{(p)}$ of an object of mass $(m)$ moving with velocity $(\vec{v})$ is given as :
$\vec{p}=m \vec{v}$
$\vec{p}=m \vec{v}$
Head on Inelastic Collision of Two Particles
Let the coefficient of restitution for collision is $e$
(i) Momentum is conserved
$m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \ldots$ (1)
(ii) Kinetic energy is not conserved.
(iii) According to Newton's law
$e=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{u}_1-\mathrm{u}_2} \ldots$ (2)
By solving eq. (1) and (2) :
$ \mathrm{v}_1=\left(\frac{\mathrm{m}_1-\mathrm{em}_2}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_1+\left(\frac{(1+e) \mathrm{m}_2}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_2=\frac{\mathrm{m}_1 \mathrm{u}_1+\mathrm{m}_2 \mathrm{u}_2-\mathrm{m}_2 e\left(\mathrm{u}_1-\mathrm{u}_2\right)}{\mathrm{m}_1+\mathrm{m}_2}$
$$ \mathrm{v}_2=\left(\frac{\mathrm{m}_2-e \mathrm{~m}_1}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_2+\left(\frac{(1+e) \mathrm{m}_1}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_1=\frac{\mathrm{m}_1 \mathrm{u}_1+\mathrm{m}_2 \mathrm{u}_2-\mathrm{m}_1 e\left(\mathrm{u}_2-\mathrm{u}_1\right)}{\mathrm{m}_1+\mathrm{m}_2} $$
(i) Momentum is conserved
$m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \ldots$ (1)
(ii) Kinetic energy is not conserved.
(iii) According to Newton's law
$e=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{u}_1-\mathrm{u}_2} \ldots$ (2)
By solving eq. (1) and (2) :
$ \mathrm{v}_1=\left(\frac{\mathrm{m}_1-\mathrm{em}_2}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_1+\left(\frac{(1+e) \mathrm{m}_2}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_2=\frac{\mathrm{m}_1 \mathrm{u}_1+\mathrm{m}_2 \mathrm{u}_2-\mathrm{m}_2 e\left(\mathrm{u}_1-\mathrm{u}_2\right)}{\mathrm{m}_1+\mathrm{m}_2}$
$$ \mathrm{v}_2=\left(\frac{\mathrm{m}_2-e \mathrm{~m}_1}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_2+\left(\frac{(1+e) \mathrm{m}_1}{\mathrm{~m}_1+\mathrm{m}_2}\right) \mathrm{u}_1=\frac{\mathrm{m}_1 \mathrm{u}_1+\mathrm{m}_2 \mathrm{u}_2-\mathrm{m}_1 e\left(\mathrm{u}_2-\mathrm{u}_1\right)}{\mathrm{m}_1+\mathrm{m}_2} $$
Finding Center of Mass of a System When Part of It's Mass is Removed
(i) $\quad \vec{r}_{\text {COM }}=\frac{m_1 \vec{r}_1-m_2 \vec{r}_2}{m_1-m_2}$ or $\vec{r}_{\text {COM }}=\frac{A_1 \vec{r}_1-A_2 \vec{r}_2}{A_1-A_2}$
(ii) $\mathrm{x}_{\operatorname{com}}=\frac{\mathrm{m}_1 \mathrm{x}_1-\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1-\mathrm{m}_2}$ or $\mathrm{x}_{\operatorname{com}}=\frac{\mathrm{A}_1 \mathrm{x}_1-\mathrm{A}_2 \mathrm{x}_2}{\mathrm{~A}_1-\mathrm{A}_2}$
$y_{\mathrm{COM}}=\frac{m_1 y_1-m_2 y_2}{m_1-m_2}$ or $y_{C O M}=\frac{A_1 y_1-A_2 y_2}{A_1-A_2}$ and
$$ \mathrm{z}_{\mathrm{COM}}=\frac{\mathrm{m}_1 \mathrm{z}_1-\mathrm{m}_2 \mathrm{z}_2}{\mathrm{~m}_1-\mathrm{m}_2} \text { or } \mathrm{z}_{\mathrm{COM}}=\frac{\mathrm{A}_1 \mathrm{z}_1-\mathrm{A}_2 \mathrm{z}_2}{\mathrm{~A}_1-\mathrm{A}_2} $$
Here, $m_1, A_1, \vec{r}_1, x_1, y_1$ and $z_1$ are the values for the whole mass while $m_2, A_2, \vec{r}_2, {x}_2, y_2$ and $z_2$ are the values for the mass which has been removed. Let us see two examples in support of the above theory.
(ii) $\mathrm{x}_{\operatorname{com}}=\frac{\mathrm{m}_1 \mathrm{x}_1-\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1-\mathrm{m}_2}$ or $\mathrm{x}_{\operatorname{com}}=\frac{\mathrm{A}_1 \mathrm{x}_1-\mathrm{A}_2 \mathrm{x}_2}{\mathrm{~A}_1-\mathrm{A}_2}$
$y_{\mathrm{COM}}=\frac{m_1 y_1-m_2 y_2}{m_1-m_2}$ or $y_{C O M}=\frac{A_1 y_1-A_2 y_2}{A_1-A_2}$ and
$$ \mathrm{z}_{\mathrm{COM}}=\frac{\mathrm{m}_1 \mathrm{z}_1-\mathrm{m}_2 \mathrm{z}_2}{\mathrm{~m}_1-\mathrm{m}_2} \text { or } \mathrm{z}_{\mathrm{COM}}=\frac{\mathrm{A}_1 \mathrm{z}_1-\mathrm{A}_2 \mathrm{z}_2}{\mathrm{~A}_1-\mathrm{A}_2} $$
Here, $m_1, A_1, \vec{r}_1, x_1, y_1$ and $z_1$ are the values for the whole mass while $m_2, A_2, \vec{r}_2, {x}_2, y_2$ and $z_2$ are the values for the mass which has been removed. Let us see two examples in support of the above theory.
POSITION OF COM OF TWO PARTICLES

X-coordinate of the centre of mass can be written as follows :
$$ X_{\mathrm{cm}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}=\frac{m_1(0)+m_2(d)}{m_1+m_2}=\frac{m_2 d}{m_1+m_2} $$
Note :
1. We know that the centre of mass of a two-particle system lies on the line joining the particles.
2. The distance of the centre of mass from particle $m_1$ is $\frac{m_2 d}{m_1+m_2}$ and so the distance of centre of mass from $m_2$ will be $d-\frac{m_2 d}{m_1+m_2}=\frac{m_1 d}{m_1+m_2}$
Impulse of Force
Impulse of force is defined as average
force multiplied with time interval for which it acts on an object.
$\vec{I}=\vec{F} \Delta t=\vec{p}_2-\vec{p}_1$
$\vec{I}=\vec{F} \Delta t=\vec{p}_2-\vec{p}_1$
Loss in Kinetic Energy in Inelastic Collision
$\Delta \mathrm{K}=\frac{\mathrm{m}_1 \mathrm{~m}_2}{2\left(\mathrm{~m}_1+\mathrm{m}_2\right)}\left(1-\mathrm{e}^2\right)\left|\mathrm{u}_1-\mathrm{u}_2\right|^2$
RECOIL OF A GUN
Before the gun is fired, both the gun and the bullet are at rest. Therefore, the total momentum of the gun-bullet system is zero. After the gun is fired, the bullet moves forward and the gun recoils backwards. Let $m_{b}$ and $m_{g}$ be the masses of the bullet and the gun. If $\mathbf{v}_{b}$ and $\mathbf{v}_{g}$ are their respective velocities after firing, the total momentum of the gun-bullet system after firing is $\left(m_{b} \mathbf{v}_{b}+m_{g} \mathbf{v}_{g}\right)$. From the law of conservation of momentum, the total momentum after and before the gun is fired must be the same, i.e.
$$ \begin{aligned} &m_{b} \mathbf{v}_{b}+m_{g} \mathbf{v}_{g}=0 \\\\ &\text { or } \quad \mathbf{v}_{g}=-\frac{m_{b} \mathbf{v}_{b}}{m_{g}} \\\\ &\text { The negative sign indicates that the gun recoils in a } \\ &\text { direction opposite to that of the bullet. In terms of mag- } \\ &\text { nitudes, we have } \end{aligned} $$
$$ v_{g}=\frac{m_{b} v_{b}}{m_{g}} $$
$$ \begin{aligned} &m_{b} \mathbf{v}_{b}+m_{g} \mathbf{v}_{g}=0 \\\\ &\text { or } \quad \mathbf{v}_{g}=-\frac{m_{b} \mathbf{v}_{b}}{m_{g}} \\\\ &\text { The negative sign indicates that the gun recoils in a } \\ &\text { direction opposite to that of the bullet. In terms of mag- } \\ &\text { nitudes, we have } \end{aligned} $$
$$ v_{g}=\frac{m_{b} v_{b}}{m_{g}} $$
CENTER OF MASS OF A UNIFORM ROD

$$ x_{com}=\frac{\int_0^L x d m}{\int d m}=\frac{\int_0^L(x)\left(\frac{M}{L} d x\right)}{M}=\frac{1}{L} \int_0^L x d x=\frac{L}{2} $$
The $y$-coordinate of COM is $y$com $=\frac{\int y d m}{\int d m}=0$.
Similarly, $z_{c o m}=0$
i.e., the coordinates of $\mathrm{COM}$ of the rod are $\left(\frac{\mathrm{L}}{2}, 0,0\right)$, i.e. it lies at the center of the rod.
Two-dimentioal or Oblique Collision

Conserving the momentum of system in directions along normal ( $x$ axis) and tangential ( $y$ axis)
Momentum conservation of x-component give
$\mathrm{m}_1 \mathrm{u}_1 \cos \alpha_1+\mathrm{m}_2 \mathrm{u}_2 \cos \alpha_2=\mathrm{m}_1 \mathrm{v}_1 \cos \beta_1+\mathrm{m}_2 \mathrm{v}_2 \cos \beta_2$
Since no force is acting on $\mathrm{m}_1$ and $\mathrm{m}_2$ along the tangent (i.e. $y$-axis) the individual momentum of $\mathrm{m}_1$ and $\mathrm{m}_2$ remains conserved.
$\mathrm{m}_1 \mathrm{u}_1 \sin \alpha_1=\mathrm{m}_1 \mathrm{v}_1 \sin \beta_1 \& \mathrm{~m}_2 \mathrm{u}_2 \sin \alpha_2=\mathrm{m}_2 \mathrm{v}_2 \sin \beta_2$
By using Newton's experimental law along the line of impact
$e=\frac{v_2 \cos \beta_2-v_1 \cos \beta_1}{u_1 \cos \alpha_1-u_2 \cos \alpha_2}$
CENTER OF MASS OF A HOLLOW HEMISPHERE

$y_{\mathrm{cm}}=\frac{\mathrm{R}}{2}$
CENTER OF MASS OF A SOLID HEMISPHERE
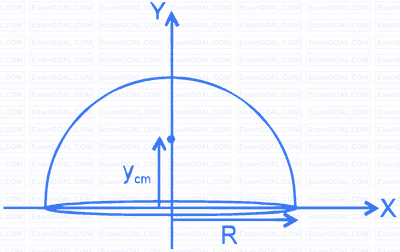
$\mathrm{y}_{\mathrm{cm}}=\frac{3 \mathrm{R}}{8}$
CENTER OF MASS OF SEMICIRCULAR DISC

$\mathrm{y}_{\mathrm{cm}}=\frac{4 \mathrm{R}}{3 \pi}$
CENTER OF MASS OF A SEMICIRCULAR RING

$\mathrm{y}_{\mathrm{cm}}=\frac{2 \mathrm{R}}{\pi}$
Momentum Conservation
Let us consider a case of $n$-particle system and total linear momentum of the system can be written as follows :
$$ \vec{P}=m_1 \vec{v}_1+m_2 \vec{v}_2+\ldots .+m_{\mathrm{n}} \vec{v}_{\mathrm{n}} $$
If $\vec{V}_{\mathrm{cm}}$ is the velocity of centre of mass of the system and $M$ is the total mass of the system then
$$ M \vec{V}_{\mathrm{cm}}=m_1 \vec{v}_1+m_2 \vec{v}_2+\ldots . .+m_{\mathrm{n}} \vec{v}_{\mathrm{n}} $$
Hence, the total linear momentum of the system can be written as follows :
$$ \vec{P}=M \vec{V}_{\mathrm{cm}} $$
On differentiating above equation we get the following relation :
$$ \begin{aligned} & \frac{d \vec{P}}{d t}=M \frac{d \vec{V}_{\mathrm{cm}}}{d t} \\\\ \Rightarrow \quad & \frac{d \vec{P}}{d t}=M \vec{a}_{\mathrm{cm}} \end{aligned} $$
We know that $\vec{F}_{\text {ext }}=M \vec{a}_{\mathrm{cm}}$;
hence above equation can be written as follows :
$$ \frac{d \vec{P}}{d t}=\vec{F}_{\text {ext }} $$
If $\vec{F}_{\text {ext }}=0 \Rightarrow $ $ \frac{d \vec{P}}{d t}=0 \Rightarrow \vec{P}=$ constant.
Thus, if no net external force acts on a system, the total linear momentum of the system remains constant; the total linear momentum being the vector sum of linear momentum of individual particles, i.e.
$$ \vec{P}=\vec{P}_1+\vec{P}_2+\cdots+\vec{P}_n $$
$$ \vec{P}=m_1 \vec{v}_1+m_2 \vec{v}_2+\ldots .+m_{\mathrm{n}} \vec{v}_{\mathrm{n}} $$
If $\vec{V}_{\mathrm{cm}}$ is the velocity of centre of mass of the system and $M$ is the total mass of the system then
$$ M \vec{V}_{\mathrm{cm}}=m_1 \vec{v}_1+m_2 \vec{v}_2+\ldots . .+m_{\mathrm{n}} \vec{v}_{\mathrm{n}} $$
Hence, the total linear momentum of the system can be written as follows :
$$ \vec{P}=M \vec{V}_{\mathrm{cm}} $$
On differentiating above equation we get the following relation :
$$ \begin{aligned} & \frac{d \vec{P}}{d t}=M \frac{d \vec{V}_{\mathrm{cm}}}{d t} \\\\ \Rightarrow \quad & \frac{d \vec{P}}{d t}=M \vec{a}_{\mathrm{cm}} \end{aligned} $$
We know that $\vec{F}_{\text {ext }}=M \vec{a}_{\mathrm{cm}}$;
hence above equation can be written as follows :
$$ \frac{d \vec{P}}{d t}=\vec{F}_{\text {ext }} $$
If $\vec{F}_{\text {ext }}=0 \Rightarrow $ $ \frac{d \vec{P}}{d t}=0 \Rightarrow \vec{P}=$ constant.
Thus, if no net external force acts on a system, the total linear momentum of the system remains constant; the total linear momentum being the vector sum of linear momentum of individual particles, i.e.
$$ \vec{P}=\vec{P}_1+\vec{P}_2+\cdots+\vec{P}_n $$
CENTER OF MASS OF A CONTINUOUS MASS DISTRIBUTION
For continuous mass distribution the center of mass can be located by replacing summation sign with an integral sign. Proper limits for the integral are chosen according to the situation
$x_{c m}=\frac{\int x d m}{\int d m}, $
$y_{c m}=\frac{\int y d m}{\int d m}, $
$z_{c m}=\frac{\int z d m}{\int d m}$
Note: If an object has symmetric mass distribution about $\mathrm{x}$ axis then $\mathrm{y}$ coordinate of COM is zero and vice-versa.
$x_{c m}=\frac{\int x d m}{\int d m}, $
$y_{c m}=\frac{\int y d m}{\int d m}, $
$z_{c m}=\frac{\int z d m}{\int d m}$
Note: If an object has symmetric mass distribution about $\mathrm{x}$ axis then $\mathrm{y}$ coordinate of COM is zero and vice-versa.
CENTER OF MASS OF A SYSTEM OF 'N' DISCRETE PARTICLES
Let $m_1, m_2, m_3, \ldots, m_{\mathrm{n}}$ be the masses of $n$ particles constituting a system. Assume that these particles are distributed in three-dimensional space and the coordinates of these particles are $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right),\left(x_3, y_3, z_3\right), \ldots \ldots\left(x_n, y_n, z_n\right)$, respectively. The location of centre of mass of the given system is mass-based average position and can be written as follows:
$$ X_{\mathrm{cm}}=\frac{m_1 x_1+m_2 x_2+m_3 x_3+\ldots+m_{\mathrm{n}} x_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} x_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}} $$
$Y_{\mathrm{cm}}=\frac{m_1 y_1+m_2 y_2+m_3 y_3+\ldots+m_{\mathrm{n}} y_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} y_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}}$
$Z_{\mathrm{cm}}=\frac{m_1 z_1+m_2 z_2+m_3 z_3+\ldots+m_{\mathrm{n}} z_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} z_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}}$
$$ X_{\mathrm{cm}}=\frac{m_1 x_1+m_2 x_2+m_3 x_3+\ldots+m_{\mathrm{n}} x_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} x_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}} $$
$Y_{\mathrm{cm}}=\frac{m_1 y_1+m_2 y_2+m_3 y_3+\ldots+m_{\mathrm{n}} y_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} y_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}}$
$Z_{\mathrm{cm}}=\frac{m_1 z_1+m_2 z_2+m_3 z_3+\ldots+m_{\mathrm{n}} z_{\mathrm{n}}}{m_1+m_2+m_3+\ldots . .+m_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^n m_{\mathrm{i}} z_{\mathrm{i}}}{\sum\limits_{i=1}^n m_{\mathrm{i}}}$
Head on collision
