Newton's First Law : If no force acts on a body, the body's velocity cannot change; that is, the body cannot accelerate.}

Newton's First Law is in terms of a net force : If no net force acts on a body $\left(\vec{F}_{\text {net }}=0\right)$, the body's velocity cannot change; that is, the body cannot accelerate.

Newton's Second Law : The net force on a body is equal to the product of the body's mass and its acceleration.

In equation form,

$$ \vec{F}_{\text {net }}=m \vec{a} \quad \text { (Newton's second law). } $$

Newton's Third Law : When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction.

When body B and body C interact with each other, we can write this law as the scalar relation

$$ F_{B C}=F_{C B} \quad \text { (equal magnitudes) } $$

Here, $$ F_{B C}$$ = Force on the body B from the body C

and $$F_{C B}$$ = Force on the body C from the body B

Or as the vector relation

$$ \vec{F}_{B C}=-\vec{F}_{C B} \quad \text { (equal magnitudes and opposite directions), } $$

When a cord (or a rope, cable, or other such object) is attached to a body and pulled taut(stretched or pulled tight, not slack), the cord pulls on the body with a force $\vec{T}$ directed away from the body and along(tangential) the cord.

Tension at point P = Weight of rope that hangs below the point P



$$ T_P=(\lambda x) g $$

where $\lambda=\frac{M}{L}$

$M=$ total mass of rope

$L=$ total length of rope and

$\lambda=$ linear mass density

Apparent reading of weighing machine in a lift

(a) When the lift moves upwards with acceleration $a: R=m(g+a)$

(b) When the lift moves downwards with acceleration $a: R=m(g-a)$

(c) When the lift falls freely: $R=0$

(d) When the lift is at rest or $a=0: R=m g$

Force applied by the spring is always opposite to the displacement produced at one end and that is why spring force is expressed as F = –Kx, where negative sign indicates that force is opposite to the displacement x.

(a) Static friction : This friction applied when body is at rest with respect to the contact surface of the body.

When body is at rest and there is no tendency in the body to move, then

Static friction, $$ \mathrm{f}_{\mathrm{s}} = F $$, where F applied force on the body

When body is about to move but at rest currently, then a constant maximum static friction force applied on the body which is prportional to normal force N,

$${\left( {{f_s}} \right)_{\max }} \propto N$$

$$ \Rightarrow $$$${\left( {{f_s}} \right)_{\max }} = {\mu _s}N$$

Here $\mu_{\mathrm{s}}$ is coefficient of static friction.

Note : Static friction force is a variable force and it is equal to applied force F when body is at rest but when body is about to move but not moving then static friction force is called maximum static friction ($${\left( {{f_s}} \right)_{\max }}$$) and equal to $\mu_{\mathrm{s}} \mathrm{N}$.

(b) Kinetic friction : This friction applied when body is moving with respect to the contact surface of the body. If the coefficient of kinetic friction is $\mu_{\mathrm{k}}$, then

When body is moving, then kinetic friction force applied on the body is also prportional to normal force N,

$${ {{f_k}} } \propto N$$

$$ \Rightarrow $$ $$ \mathrm{f}_{\mathrm{k}} = \mu_{\mathrm{k}} \mathrm{N} $$

Note : Kinetic friction force is a constant force and it is always equal to $\mu_{\mathrm{k}} \mathrm{N}$.

Angle of repose is the minimum angle of inclination of a plane with the horizontal so that object placed on it just begins to slide down.



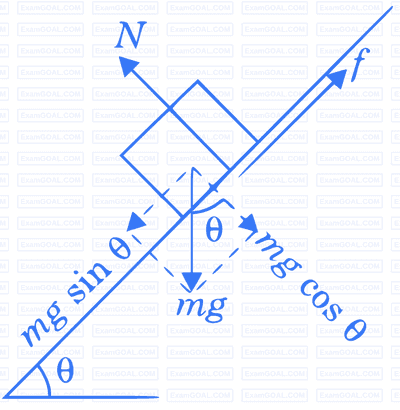
$$ N=m g \cos \theta $$

When the block is not sliding down the plane then we can write the following equation:

$f=m g \sin \theta$

If µ is the coefficient of friction between the block and inclined plane then maximum possible magnitude of friction can be written as follows :

$$ f_{\max }=\mu N=\mu m g \cos \theta $$

At a particular value of $\theta_0$ driving force $m g \sin \theta_0$ becomes equal to maximum opposing force $\mu m g \cos \theta_0$. Here angle $\theta_0$ is the angle of repose for this block and plane.

$\therefore \quad m g \sin \theta_0=\mu m g \cos \theta_0$

$\Rightarrow \quad \tan \theta_0=\mu$

$\Rightarrow \quad \theta_0=\tan ^{-1}(\mu)$

For a body placed on inclined plane of inclination $\theta$

(a) Normal reaction :

$$ N=m g \cos \theta $$

(b) Friction :

$$ f=\mu N=\mu m g \cos \theta $$

(c) When a body moves down, its acceleration is

$$ a=g(\sin \theta-\mu \cos \theta) $$

(d) When a body moves up, its acceleration is

$$ a=g(\sin \theta+\mu \cos \theta) $$