ROTATIONAL EQUILIBRIUM
If a rigid body is in rotational equilibrium under the action of several coplanar forces, the resultant torque of all the forces about any axis perpendicular to the plane containing the forces must be zero.
In the figure a body is shown under the action of several external coplanar forces $F_1, F_2, \ldots . . F_i$ and $F_n$.
$$\sum {\overrightarrow \tau } $$ = 0
$$\sum {\overrightarrow \tau } $$ = 0
Angular Momentum of a Rigid Body
For a rigid body rotating about a fixed axis, the component of its angular momentum parallel to the rotation axis is
KINETIC ENERGY OF ROTATING BODIES AND MOMENT OF INERTIA
Consider a system of point masses rotating with angular velocity about a fixed axis through . Kinetic energy of a point mass located at distant from the centre is given by:
Kinetic energy of the system
The expression is known as moment of inertia of the system about the corresponding axis. It is denoted by .
Hence kinetic energy of the system =
Kinetic energy of the system
The expression is known as moment of inertia of the system about the corresponding axis. It is denoted by .
Hence kinetic energy of the system =
The Parallel-Axis Theorem
The parallel-axis theorem relates the rotational or moments of inertia of a body about any axis to that of the same body about a parallel axis through the center of mass :
Here is the perpendicular distance between the two axes.
Here is the perpendicular distance between the two axes.
Newton's Second Law in Angular Form
Newton's second law for a particle can be written in angular form as
$$ \vec{\tau}_{\text {net }}=\frac{d \vec{\ell}}{d t}, $$
where $\vec{\tau}_{\text {net }}$ is the net torque acting on the particle and $\vec{\ell}$ is the angular momentum of the particle.
$$ \vec{\tau}_{\text {net }}=\frac{d \vec{\ell}}{d t}, $$
where $\vec{\tau}_{\text {net }}$ is the net torque acting on the particle and $\vec{\ell}$ is the angular momentum of the particle.
Work and Rotational Kinetic Energy
Thin Rod
Position of the axis of rotation :
(a) About an axis passing through centre of mass and perpendicular to its length
(b)

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through one end and perpendicular to length of the rod
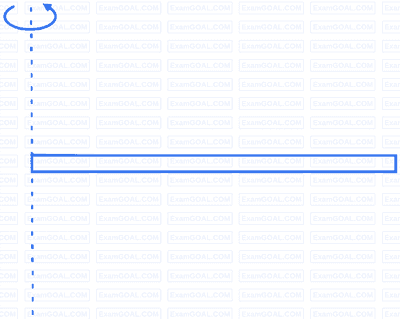
Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through one end and perpendicular to length of the rod

Moment of Inertia (I) =
Radius of gyration (K) =
TORQUE
Torque about point :

Magnitude of torque Force perpendicular distance of line of action of force from the axis of rotation.
Direction of torque can be determined by using right hand thumb rule.

Magnitude of torque Force perpendicular distance of line of action of force from the axis of rotation.
Direction of torque can be determined by using right hand thumb rule.
Radius of Gyration (K)
has no meaning without axis of rotation.
is a scalar quantity
Radius of gyaration
is a scalar quantity
Radius of gyaration
Moment of Inertia for Rigid Bodies

Moment of inertia of a rigid body about any axis of rotation.
Solid Sphere
Position of the axis of rotation :
About its diametric
axis which passes
through its centre
of mass

Moment of Inertia (I) = $${2 \over 5}M{R^2}$$
Radius of gyration (K) = $$\sqrt {{2 \over 5}} R$$
Position of the axis of rotation : About a tangent to the sphere

Moment of Inertia (I) = $${7 \over 5}M{R^2}$$
Radius of gyration (K) = $$\sqrt {{7 \over 5}} R$$

Moment of Inertia (I) = $${2 \over 5}M{R^2}$$
Radius of gyration (K) = $$\sqrt {{2 \over 5}} R$$
Position of the axis of rotation : About a tangent to the sphere

Moment of Inertia (I) = $${7 \over 5}M{R^2}$$
Radius of gyration (K) = $$\sqrt {{7 \over 5}} R$$
Angular Momentum of a System of Particles
The angular momentum $\vec{L}$ of a system of particles is the vector sum of the angular momenta of the individual particles:
$$ \vec{L}=\vec{\ell}_1+\vec{\ell}_2+\cdots+\vec{\ell}_n=\sum\limits_{i=1}^n \vec{\ell}_i . $$
The time rate of change of this angular momentum is equal to the net external torque on the system (the vector sum of the torques due to interactions with particles external to the system):
$$ \vec{\tau}_{\text {net }}=\frac{d \vec{L}}{d t} \quad \text { (system of particles). } $$
$$ \vec{L}=\vec{\ell}_1+\vec{\ell}_2+\cdots+\vec{\ell}_n=\sum\limits_{i=1}^n \vec{\ell}_i . $$
The time rate of change of this angular momentum is equal to the net external torque on the system (the vector sum of the torques due to interactions with particles external to the system):
$$ \vec{\tau}_{\text {net }}=\frac{d \vec{L}}{d t} \quad \text { (system of particles). } $$
Moment of Inertia of System of Particle

Hollow Cylinder
Position of the axis of rotation :
About its geometrical axis which is parallel to
its length
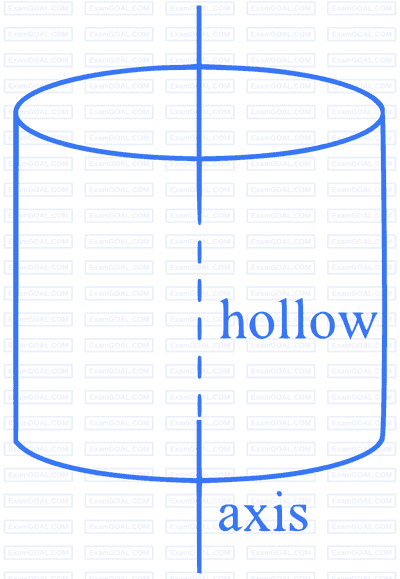
Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis which is perpendicular to its length and passes through its centre of mass
Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis which is perpendicular to its length and passes through its centre of mass
Moment of Inertia (I) =
Radius of gyration (K) =
Perpendicular axis Theorems
(body lies on the plane)

Note : (Valid only for 2-dimensional body)
Hollow Sphere
Position of the axis of rotation :
About diametric axis passing through centre of mass

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About a tangent to the surface

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About a tangent to the surface

Moment of Inertia (I) =
Radius of gyration (K) =
Kinetic Energy in case of mixed Translational and Rotational Motion
Moment of Inertia of a Particle
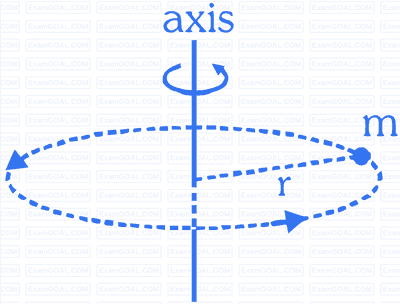
The moment of inertia of a particles with respect to an axis of rotation is equal to the product of mass of the particle and square of distance from rotational axis.
perpendicular distance from axis of rotation
Annular Cylinder (or Ring)
Position of the axis of rotation :
About an axis perpendicular to the plane and passes through the centre

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About the diametric axis
Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About the diametric axis
Moment of Inertia (I) =
Radius of gyration (K) =
Circular Disc
Position of the axis of rotation :
About an axis perpendicular to the plane and passes through the centre

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About the diametric axis

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About the diametric axis

Moment of Inertia (I) =
Radius of gyration (K) =
Conservation of Angular Momentum
The angular momentum $\vec{L}$ of a system remains constant if the net external torque acting on the system is zero:
$
\vec{L} =\text { a constant } \text { (isolated system) } $
$ \text { or } \vec{L}_i =\vec{L}_f \quad \text { (isolated system). } $
This is the law of conservation of angular momentum.
$ \text { or } \vec{L}_i =\vec{L}_f \quad \text { (isolated system). } $
This is the law of conservation of angular momentum.
Angular Momentum of a Particle
The angular momentum $\vec{\ell}$ of a particle with linear momentum $\vec{p}$, mass $m$, and linear velocity $\vec{v}$ is a vector quantity defined relative to a fixed point (usually an origin) as
$$ \vec{\ell}=\vec{r} \times \vec{p}=m(\vec{r} \times \vec{v}) $$
The magnitude of $\vec{\ell}$ is given by
$$ \begin{aligned} \ell &=r m v \sin \phi \\\\ &=r p_{\perp}=r m v_{\perp} \\\\ &=r_{\perp} p=r_{\perp} m v, \end{aligned} $$
where $\phi$ is the angle between $\vec{r}$ and $\vec{p}, p_{\perp}$ and $v_{\perp}$ are the components of $\vec{p}$ and $\vec{v}$ perpendicular to $\vec{r}$, and $r_{\perp}$ is the perpendicular distance between the fixed point and the extension of $\vec{p}$. The direction of $\ell$ is given by the right-hand rule for cross products.
$$ \vec{\ell}=\vec{r} \times \vec{p}=m(\vec{r} \times \vec{v}) $$
The magnitude of $\vec{\ell}$ is given by
$$ \begin{aligned} \ell &=r m v \sin \phi \\\\ &=r p_{\perp}=r m v_{\perp} \\\\ &=r_{\perp} p=r_{\perp} m v, \end{aligned} $$
where $\phi$ is the angle between $\vec{r}$ and $\vec{p}, p_{\perp}$ and $v_{\perp}$ are the components of $\vec{p}$ and $\vec{v}$ perpendicular to $\vec{r}$, and $r_{\perp}$ is the perpendicular distance between the fixed point and the extension of $\vec{p}$. The direction of $\ell$ is given by the right-hand rule for cross products.
RELATION BETWEEN TORQUE AND ANGULAR ACCELERATION
The rotational analog of Newton's second law is
$$ \tau_{\text {net }}=I \alpha, $$
where $\tau_{\text {net }}$ is the net torque acting on a particle or rigid body, $I$ is the rotational inertia of the particle or body about the rotation axis, and $\alpha$ is the resulting angular acceleration about that axis.
$$ \tau_{\text {net }}=I \alpha, $$
where $\tau_{\text {net }}$ is the net torque acting on a particle or rigid body, $I$ is the rotational inertia of the particle or body about the rotation axis, and $\alpha$ is the resulting angular acceleration about that axis.
Cube
Position of the axis of rotation :
About its geometrical axis, which is along its length

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Rectangular Plate
Position of the axis of rotation : About an axis passing through centre of mass and perpendicular to side in its plane

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through centre of mass and perpendicular to side a in its plane.

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing throught centre of mass and perpendicular to plane

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through centre of mass and perpendicular to side a in its plane.

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing throught centre of mass and perpendicular to plane

Moment of Inertia (I) =
Radius of gyration (K) =
Solid Cylinder
Position of the axis of rotation :
About its geometrical axis, which is along its length

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis tangential to the cylinderical surface and parallel to its geometrical axis is perpendicular to its length and passes through its centre of mass

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through the centre of mass and perpendicular to its length

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis tangential to the cylinderical surface and parallel to its geometrical axis is perpendicular to its length and passes through its centre of mass

Moment of Inertia (I) =
Radius of gyration (K) =
Position of the axis of rotation : About an axis passing through the centre of mass and perpendicular to its length

Moment of Inertia (I) =
Radius of gyration (K) =
Circular Ring
Position of the axis of rotation :
About an axis perpendicular to the plane and passes through the centre

Moment of Inertia (I) = MR2
Radius of gyration (K) = R
Position of the axis of rotation : About the diametric axis

Moment of Inertia (I) =
Radius of gyration (K) =

Moment of Inertia (I) = MR2
Radius of gyration (K) = R
Position of the axis of rotation : About the diametric axis

Moment of Inertia (I) =
Radius of gyration (K) =