Average Velocity (in an interval)
Average Velocity $=\frac{\text { displacement }}{\text { timeinterval }}$
For straight line motion, along $x$-axis, we have
$$ \mathrm{v}_{\mathrm{av}}=\overline{\mathrm{v}}=\langle\mathrm{v}\rangle=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{x}_{\mathrm{f}}-\mathrm{x}_{\mathrm{i}}}{\mathrm{t}_{\mathrm{f}}-\mathrm{t}_{\mathrm{i}}} $$
For straight line motion, along $x$-axis, we have
$$ \mathrm{v}_{\mathrm{av}}=\overline{\mathrm{v}}=\langle\mathrm{v}\rangle=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{x}_{\mathrm{f}}-\mathrm{x}_{\mathrm{i}}}{\mathrm{t}_{\mathrm{f}}-\mathrm{t}_{\mathrm{i}}} $$
Instantaneous Velocity (at an instant)
The velocity at a particular instant of time is known as instantaneous velocity. The term "velocity" usually means instantaneous velocity.
$$ V_{\text {inst. }}=\lim \limits_{\Delta t \rightarrow 0}\left(\frac{\Delta x}{\Delta t}\right)=\frac{d x}{d t} $$
$$ V_{\text {inst. }}=\lim \limits_{\Delta t \rightarrow 0}\left(\frac{\Delta x}{\Delta t}\right)=\frac{d x}{d t} $$
Position
The position of a particle refers to its location in the space at a certain moment of time.
Displacement
The change in the position of a moving object is known as displacement.
The change in position vector of a particle going from initial position (say $i$ ) to final position (say $f$ ) is called Displacement or Relative Position Vector of the particle. It is denoted by $\Delta \vec{r}$, such that
$$ \Delta \vec{r}=\vec{r}_f-\vec{r}_i $$

The change in position vector of a particle going from initial position (say $i$ ) to final position (say $f$ ) is called Displacement or Relative Position Vector of the particle. It is denoted by $\Delta \vec{r}$, such that
$$ \Delta \vec{r}=\vec{r}_f-\vec{r}_i $$

Distance
The length of the actual path travelled by a particle during a given time interval is called as distance.
Average Speed (in an interval)
$$
\text { Average Speed }=\frac{\text { distance travelled }}{\text { time interval }}
$$
The dimension of velocity is $\left[\mathrm{LT}^{-1}\right]$ and its $\mathrm{SI}$ unit is $\mathrm{m} / \mathrm{s}$.
The dimension of velocity is $\left[\mathrm{LT}^{-1}\right]$ and its $\mathrm{SI}$ unit is $\mathrm{m} / \mathrm{s}$.
Average acceleration (in an interval)
Average acceleration $=\frac{\text { change in velocity }}{\text { time interval }}$
Average acceleration is a vector quantity whose direction is same as that of the change in velocity.
$$ \overrightarrow{\mathrm{a}}_{\mathrm{av}}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\overrightarrow{\mathrm{v}}_{\mathrm{f}}-\overrightarrow{\mathrm{v}}_{\mathrm{i}}}{\Delta \mathrm{t}} $$
Since for a straight line motion the velocities are along a line, therefore
$$ \mathrm{a}_{\mathrm{av}}=\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}=\frac{\mathrm{v}_{\mathrm{f}}-\mathrm{v}_{\mathrm{i}}}{\mathrm{t}_{\mathrm{f}}-\mathrm{t}_{\mathrm{i}}} $$
Average acceleration is a vector quantity whose direction is same as that of the change in velocity.
$$ \overrightarrow{\mathrm{a}}_{\mathrm{av}}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\overrightarrow{\mathrm{v}}_{\mathrm{f}}-\overrightarrow{\mathrm{v}}_{\mathrm{i}}}{\Delta \mathrm{t}} $$
Since for a straight line motion the velocities are along a line, therefore
$$ \mathrm{a}_{\mathrm{av}}=\frac{\Delta \mathrm{v}}{\Delta \mathrm{t}}=\frac{\mathrm{v}_{\mathrm{f}}-\mathrm{v}_{\mathrm{i}}}{\mathrm{t}_{\mathrm{f}}-\mathrm{t}_{\mathrm{i}}} $$
Instantaneous Acceleration (at an instant)
The instantaneous acceleration of a particle is its acceleration at a particular instant of time.
Instantaneous Acceleration is
$$ \vec{a}_{\mathrm{ins}}=\vec{a}=\lim \limits_{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{d \vec{v}}{d t} $$
So, $\vec{a}=\frac{d \vec{v}}{d t}=\frac{d^2 \vec{x}}{d t^2}$
Instantaneous Acceleration is
$$ \vec{a}_{\mathrm{ins}}=\vec{a}=\lim \limits_{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{d \vec{v}}{d t} $$
So, $\vec{a}=\frac{d \vec{v}}{d t}=\frac{d^2 \vec{x}}{d t^2}$
UNIFORMLY ACCELERATED MOTION SYSTEMS
Consider a particle moving in a straight line with constant acceleration $a$. If $u$ is the initial velocity, $v$ is the velocity at time $t, s$ is the displacement $(=\Delta x)$ in time $t$ and $s_n^{\text {th }}$ is the displacement in the $n^{\text {th }}$ second of motion, then equations governing the motion of such a particle are
$$ \begin{aligned} &v=u+a t \\\\ &s=\Delta x=u t+\frac{1}{2} a t^2 \\\\ &v^2-u^2=2 a s \\\\ &s=\frac{u+v}{2} t \\\\ &s_n^{\text {th }}=u+\frac{1}{2} a(2 n-1) \end{aligned} $$
$$ \begin{aligned} &v=u+a t \\\\ &s=\Delta x=u t+\frac{1}{2} a t^2 \\\\ &v^2-u^2=2 a s \\\\ &s=\frac{u+v}{2} t \\\\ &s_n^{\text {th }}=u+\frac{1}{2} a(2 n-1) \end{aligned} $$
Graphs in Uniformly Accelerated Motion (a ≠ 0)
(a) a - t graph : If acceleration a is constant, then a t- graph is a horizontal line as shown.

(b) v - t graph : For constant acceleration, v is a linear polynomial in terms of t . Hence v t- graph is a straight line of slope a as shown.

(c) x - t graph : For constant acceleration, x is a quadratic polynomial in terms of t . Hence x t- graph is a parabola.
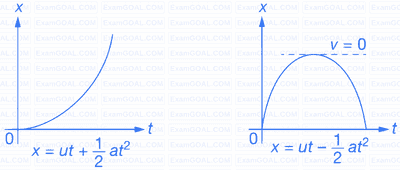

Position vs Time Graph
(1) Zero Velocity : As position of particle is fixed at all the times, so the body is at rest.
Slope
Velocity of particle is zero.

(2) Uniform Velocity : Here is constant.
so, constant
Velocity of particle is constant.
(3) Non Uniform Velocity (Increasing with Time): In this case, as time is increasing, is also increasing.
Hence, velocity of particle is increasing.

(4) Non Uniform Velocity (Decreasing with Time) : In this case, as time increases, decreases.
also decreases.
Hence, velocity of particle is decreasing.

Slope
Velocity of particle is zero.

(2) Uniform Velocity : Here is constant.
so, constant
Velocity of particle is constant.

(3) Non Uniform Velocity (Increasing with Time): In this case, as time is increasing, is also increasing.
Hence, velocity of particle is increasing.

(4) Non Uniform Velocity (Decreasing with Time) : In this case, as time increases, decreases.
also decreases.
Hence, velocity of particle is decreasing.

Velocity vs Time Graph
(1) Zero Acceleration : Velocity is constant
Hence, acceleration is zero i.e., graph is a straight line parallel to time axis.

(2) Uniform Acceleration : is constant
constant
i.e., - graph is a straight line with positive slope.

(3) Uniform Retardation : Since ,
is constant and negative.
negative constant
i.e., graph is a straight line with negative slope.

Hence, acceleration is zero i.e., graph is a straight line parallel to time axis.

(2) Uniform Acceleration : is constant
constant
i.e., - graph is a straight line with positive slope.

(3) Uniform Retardation : Since ,
is constant and negative.
negative constant
i.e., graph is a straight line with negative slope.

Acceleration vs Time Graph
(1) Constant Acceleration :
Hence acceleration is constant i.e., graph is a straight line parallel to time axis.

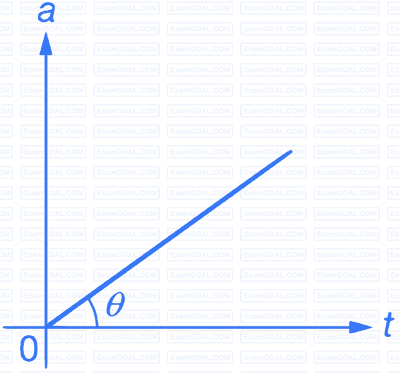
(2) Uniformly Increasing Acceleration : is constant.
Hence, acceleration is uniformly increasing with time i.e., graph is a straight line with positive slope.
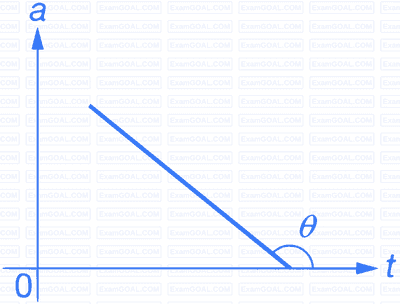
(3) Uniformly Decreasing Acceleration : Since
is constant and negative
negative constant
Hence, acceleration is uniformly decreasing with time i.e., graph is a straight line with negative slope.
Hence acceleration is constant i.e., graph is a straight line parallel to time axis.

(2) Uniformly Increasing Acceleration : is constant.
Hence, acceleration is uniformly increasing with time i.e., graph is a straight line with positive slope.

(3) Uniformly Decreasing Acceleration : Since
is constant and negative
negative constant
Hence, acceleration is uniformly decreasing with time i.e., graph is a straight line with negative slope.

Important Note 1 :
Slopes of v - t or s - t graphs can never be infinite
at any point, because infinite slope of v - t graph
means infinite acceleration. Similarly, infinite
slope of s - t graph means infinite velocity. Hence,
the following graphs are not possible :


Important Note 2 :
At one time, two values of velocity or displacement are not possible. Hence, the following
graphs are not right :


VERTICAL MOTION UNDER GRAVITY
1.
Take initial direction of motion of the particle as positive.
Example :
(a) If a particle is dropped from a tower, then we can take downward direction (the direction of initial motion) as positive.
(b) If a particle is thrown vertically upwards from a tower, then we can take upward direction (the direction of initial motion) as positive.
2.
The quantities ( i.e. u , v , a and s ) along the initial direction of motion will be taken as positive whereas opposite to the initial direction of motion are taken as negative.
For example :
(a) For the particle dropped from the tower of height h, we have taken downward direction (the direction of initial motion) as positive. So, in this case we have
u = 0, v = +v , a = +g and s = +h as all are in the downward direction.
(b) For the particle thrown vertically upwards from a tower of height h, we have taken upward direction (the direction of initial motion) as positive. So, in this case, since
• initial velocity u is upwards, so u = +u ,
• acceleration due to gravity is downwards, so a = -g
3.
Now you can apply the equations of all one dimensional motion of the particle.
Take initial direction of motion of the particle as positive.
Example :
(a) If a particle is dropped from a tower, then we can take downward direction (the direction of initial motion) as positive.
(b) If a particle is thrown vertically upwards from a tower, then we can take upward direction (the direction of initial motion) as positive.
2.
The quantities ( i.e. u , v , a and s ) along the initial direction of motion will be taken as positive whereas opposite to the initial direction of motion are taken as negative.
For example :
(a) For the particle dropped from the tower of height h, we have taken downward direction (the direction of initial motion) as positive. So, in this case we have
u = 0, v = +v , a = +g and s = +h as all are in the downward direction.
(b) For the particle thrown vertically upwards from a tower of height h, we have taken upward direction (the direction of initial motion) as positive. So, in this case, since
• initial velocity u is upwards, so u = +u ,
• acceleration due to gravity is downwards, so a = -g
3.
Now you can apply the equations of all one dimensional motion of the particle.